Question

in the following ordinary annuity interest is compounded with each payment and the payment is made at the end of the compounding period. find the accumulated amount of the annuity. 4,500 annually at 6% for 10 years

Answer 1

Answer: $59313.58

Explanation:

Formula to find the accumulated amount of the annuity is given by :-

`FV=A(((1+(r)/(m))^(mt))-1)/((r)/(m)))`

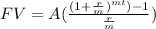
, where A is the annuity payment deposit, r is annual interest rate , t is time in years and m is number of periods.

Given : m= $2000 ; m= 1 [∵ its annual] ; t= 10 years ; r= 0.06

Now substitute all these value in the formula , we get

`FV=(4500)(((1+(0.06)/(1))^(1*10))-1)/((0.06)/(1)))`

⇒
`FV=(4500)(((1.06)^(10))-1)/(0.06))`

⇒
`FV=(4500)((0.79084769654)/(0.06))`

⇒
`FV=(4500)(13.1807949423)`

⇒
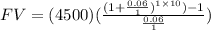
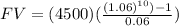
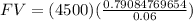
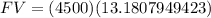
`FV=59313.5772407\approx59313.58 \ \ \text{ [Rounded to the nearest cent]}`

Hence, the accumulated amount of the annuity= $59313.58