Answer:
In 17th year, his income was $30,700.
Explanation:
It is given that the income has been increasing each year by the same dollar amount. It means it is linear function.
Income in first year = $17,900
Income in 4th year = $20,300
Let y be the income at x year.
It means the line passes through the point (1,17900) and (4,20300).
If a line passes through two points
 and
and
 , then the equation of line is
, then the equation of line is
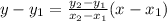
The equation of line is
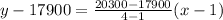
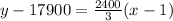
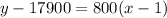
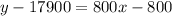
Add 17900 on both sides.
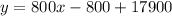

The income equation is y=800x+17100.
Substitute y=30,700 in the above equation.
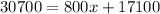
Subtract 17100 from both sides.
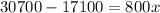
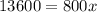
Divide both sides by 800.
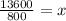
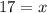
Therefore, in 17th year his income was $30,700.