Question

At one instant a bicyclist is 21.0 m due east of a park's flagpole, going due south with a speed of 13.0 m/s. Then 21.0 s later, the cyclist is 21.0 m due north of the flagpole, going due east with a speed of 13.0 m/s. For the cyclist in this 21.0 s interval, what are the (a) magnitude and (b) direction of the displacement, the (c) magnitude and (d) direction of the average velocity, and the (e) magnitude and (f) direction of the average acceleration? (Give all directions as positive angles relative to due east, where positive is meaured going counterclockwise.)

Answer 1

Part a)

`d = 21\sqrt2 = 29.7 m`

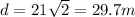
Part b)

Direction is 45 degree North of West

Part c)

`v_(avg) = 1.41 m/s`

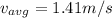
Part d)

direction of velocity will be 45 Degree North of West

Part e)

`a = 0.875 m/s^2`

Part f)

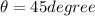`\theta = 45 degree` North of East

Step-by-step explanation:

Initial position of the cyclist is given as

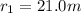`r_1 = 21.0 m` due East

final position of the cyclist after t = 21.0 s

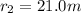`r_2 = 21.0 m` due North

Part a)

for displacement we can find the change in the position of the cyclist

so we have

`d = r_2 - r_1`

`d = 21\hat j - 21\hat i`

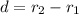
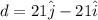
so magnitude of the displacement is given as

`d = 21\sqrt2 = 29.7 m`

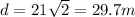
Part b)

direction of the displacement is given as

`\theta = tan^(-1)(y)/(x)`

`\theta = tan^(-1)(21)/(-21)`

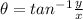
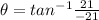
so it is 45 degree North of West

Part c)

For average velocity we know that it is defined as the ratio of displacement and time

so here the magnitude of average velocity is defined as

`v_(avg) = (\Delta x)/(t)`

`v_(avg) = (29.7)/(21)`

`v_(avg) = 1.41 m/s`

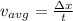
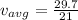
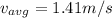
Part d)

As we know that average velocity direction is always same as that of average displacement direction

so here direction of displacement will be 45 Degree North of West

Part e)

Here we also know that initial velocity of the cyclist is 13 m/s due South while after t = 21 s its velocity is 13 m/s due East

So we have

change in velocity of the cyclist is given as

`\Delta v = v_f - v_i`

`\Delta v = 13\hat i - (-13\hat j)`

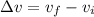
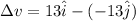
now average acceleration is given as

`a = (\Delta v)/(\Delta t)`

`a = (13\hat i + 13\hat j)/(21)`

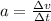
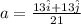
so the magnitude of acceleration is given as

`a = (13\sqrt2)/(21) = 0.875 m/s^2`

Part f)

direction of acceleration is given as

`\theta = tan^(-1)(y)/(x)`

`\theta = tan^(-1)(13)/(13)`

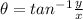
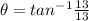
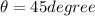`\theta = 45 degree` North of East