Question

Convert the following systems of equations to an augmented matrix and use Gauss-Jordan reduction to convert to an equilivalent matrix in reduced row echelon form. (Show the steps in the process of converting to G-J). You don't have to find the solution set X12x223 = 6 2a1 3 = 6 X1x23x3 = 6

Answer 1

System of equations:

`x_1+2x_2+2x_3=6\\2x_1+x_2+x_3=6\\x_1+x_2+3x_3=6`

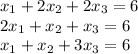
Augmented matrix:

`\left[\begin{array}{cccc}1&2&2&6\\2&1&1&6\\1&1&3&6\end{array}\right]`

Reduced Row Echelon matrix:

`\left[\begin{array}{cccc}1&2&2&6\\0&1&1&2\\0&0&1&1\end{array}\right]`

Explanation:

Convert the system into an augmented matrix:

`\left[\begin{array}{cccc}1&2&2&6\\2&1&1&6\\1&1&3&6\end{array}\right]`

For notation, R_n is the new nth row and r_n the unchanged one.

1. Operations:

`R_2=-2r_1+r_2\\R_3=-r_1+r_3`

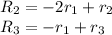
Resulting matrix:

`\left[\begin{array}{cccc}1&2&2&6\\0&-3&-3&-6\\0&-1&1&0\end{array}\right]`

2. Operations:

`R_2=-(1)/(3)r_2`

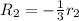
Resulting matrix:

`\left[\begin{array}{cccc}1&2&2&6\\0&1&1&2\\0&-1&1&0\end{array}\right]`

3. Operations:

`R_3=r_2+r_3`

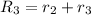
Resulting matrix:

`\left[\begin{array}{cccc}1&2&2&6\\0&1&1&2\\0&0&2&2\end{array}\right]`

4. Operations:

`R_3=(1)/(2)r_3`

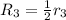
Resulting matrix:

`\left[\begin{array}{cccc}1&2&2&6\\0&1&1&2\\0&0&1&1\end{array}\right]`