Question

(b) What's the largest product possible from two numbers adding up to 100?

Answer 1

2500

Explanation:

We have to find the largest product of two numbers whose sum is 100.

Let the two numbers be x and y.

Thus, we can write x+y=100

We can calculate the value of y as:

y = 100 - x

The product of these number can be written as: (x)(y) = (x)(100-x) = 100x - x²

Let f(x) = 100x - x²

Now, the first derivative of this function with respect to x is

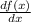`(df(x))/(dx)` = 100-2x

Equating
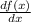`(df(x))/(dx)` = 0, we get,

100-2x = 0

⇒ x = 50

Now, we find the second derivative of the the function f(x) with respect to x

`(d^2f(x))/(dx^2)` = -2

Since,
`(d^2f(x))/(dx^2)` < 0, then by double derivative test the function have a local maxima at x = 50

This, x = 50 and y = 100-50 =50

Largest product = (50)(50) = 2500