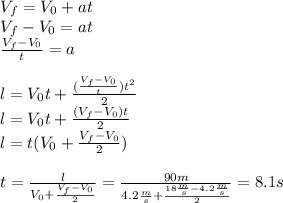Question

A skier is gliding along at 4.2 m/s on horizontal, frictionless snow. He suddenly starts down a 10° incline. His speed at the bottom is 18 m/s . a) What is the length of the incline?

Express your answer with the appropriate units.

b) How long does it take him to reach the bottom?
Express your answer with the appropriate units.

Answer 1

a) 90m

b) 8.1s

Step-by-step explanation:

The shortest way to finding the length of the incline is to apply an energetic analysis to determine the height of the incline. At the beginning, there is potential and kinetic energy that will turn into kinetic energy only:

`mgh+(1)/(2)mv_(0)^(2) =(1)/(2)mv_(f)^(2)`

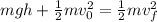
Before we input any information, let's solve for h:

`mgh+(1)/(2)mv_(0)^(2) =(1)/(2)mv_(f)^(2)}\\\\m(gh+(v_(0)^(2))/(2))=(1)/(2)mv_(f)^(2)}\\\\gh+(v_(0)^(2))/(2)=(v_(f)^(2))/(2)\\\\gh=(1)/(2)(v_(0)^(2)-v_(f)^(2))\\\\h=(1)/(2g)(v_(0)^(2)-v_(f)^(2))=(1)/(2*9.8(m)/(s^(2)))(4.2(m)/(s)^(2)-18(m)/(s)^(2))=15.63m`

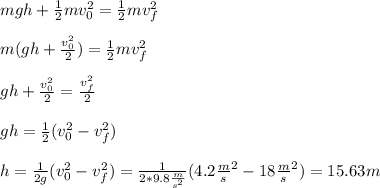
Using a sine formula we can solve for
`l`:

`Sin(10)=(h)/(l)\\\\l=(h)/(Sin(10))=(15.63m)/(0.17)=90m`

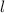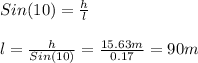
In order to find the time we will use the distance formula and final velocity formula as a system of equations to solve for t:

`X=V_(0)t+(at^2)/(2)\\\\V_f=V_0+at`

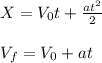
Since the acceleration and time are both variables we will solve for acceleration in the final velocity formula and replace in the distance formula:

`V_f=V_0+at\\V_f-V_0=at\\(V_f-V_0)/(t)=a\\\\l=V_0t+(((V_f-V_0)/(t))t^2)/(2)\\l=V_0t+((V_f-V_0)t)/(2)\\l=t(V_0+(V_f-V_0)/(2))\\\\t=(l)/(V_0+(V_f-V_0)/(2))=(90m)/(4.2(m)/(s)+(18(m)/(s)-4.2(m)/(s))/(2))=8.1s`