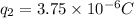Answer:
Part a)
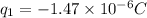
Part b)
Step-by-step explanation:
Let the charge on two spheres is q1 and q2
now the force between two charges are
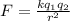
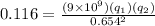
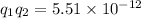
now when we connect then with conducting wire then both sphere will equally divide the charge
so we will have
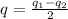
now we have
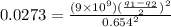
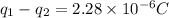
now we will have
Now we can solve above two equations
Part a)
negative charge on the sphere is
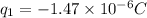
Part b)
positive charge on the sphere is