Question

An infinitely long line charge of uniform linear charge density λ = -3.00 µC/m lies parallel to the y axis at x = -3.00 m. A point charge of 3.00 µC is located at x = 1.00 m, y = 2.00 m. Find the electric field at x = 2.00 m, y = 1.50 m.

Answer 1

E=[8.1X-9.63Y]*10^{3}N/m

Step-by-step explanation:

Field in the point is the sum of the point charge electric field and the field of the infinite line.

First, we calculate the point charge field:

`E_(Charge)=(1)/(4\pi \epsilon_0)  *(Q)/(||r_p -r||^2) *Unitary vector\\||r_p -r||^2=(x_p-x)^2+(y_p -y)^2=1.25 m^2\\Unitary Vector=((r_p -r))/(||r_p -r||)=((x_p-x)X+(y_p -y)Y)/(||r_p -r||)\\=(2√(5) )/(5)X- (√(5) )/(5)Y \\E_(Charge)=K*(3\mu C)/(1.25m^2)*((2√(5) )/(5)X- (√(5) )/(5)Y)`

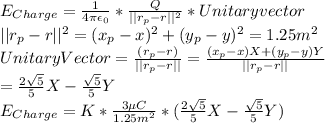
It is vectorial, where X and Y represent unitary vectors in X and Y. we recall the Coulomb constant k=
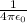`(1)/(4\pi \epsilon_0)` and not replace it yet. Now we compute the line field as follows:

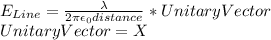`E_(Line)=(\lambda)/(2\pi \epsilon_0 distance) *Unitary Vector\\Unitary Vector=X` (The field is only in the perpendicular direction to the wire, which is X)

`E_(Line)=(-3\mu C/m*2)/(2*2\pi \epsilon_0 5*m)X=K*(6\mu C/m)/( 5*m)(-X)`

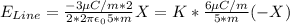
We multiplied by 2/2 in order to obtain Coulomb constant and express it that way. Finally, we proceed to sum the fields.

`E=K*(3\mu C)/(1.25m^2)*((2√(5) )/(5)X- (√(5) )/(5)Y)+K*(6\mu C)/( 5*m^2)(-X)\\E=K*[2.15-1.2]X-K*[1.07]Y \mu N/m\\E=K*[0.9X-1.07Y] \mu C/m^2\\E=[8.1X-9.63Y]*10^(3)N/m`