Question

A basic cellular phone plan costs $4 per month for 70 calling minutes. Additional time costs $0.10 per minute. The formula C= 4+0.10(x-70) gives the monthly cost for this plan, C, for x calling minutes, where x>70. How many calling minutes are possible for a monthly cost of at least $7 and at most $8?

Answer 1

For a monthly cost of at least $7 and at most $8, you can have between 100 and 110 calling minutes.

Explanation:

The problem states that the monthly cost of a celular plan is modeled by the following function:

`C(x) = 4 + 0.10(x-70)`

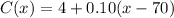
In which C(x) is the monthly cost and x is the number of calling minutes.

How many calling minutes are needed for a monthly cost of at least $7?

This can be solved by the following inequality:

`C(x) \geq 7`

`4 + 0.10(x - 70) \geq 7`

`4 + 0.10x - 7 \geq 7`

`0.10x \geq 10`

`x \geq (10)/(0.1)`

`x \geq 100`

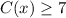
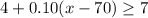
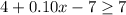
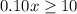
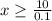
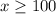
For a monthly cost of at least $7, you need to have at least 100 calling minutes.

How many calling minutes are needed for a monthly cost of at most 8:

`C(x) \leq 8`

`4 + 0.10(x - 70) \leq 8`

`4 + 0.10x - 7 \leq 8`

`0.10x \leq 11`

`x \leq (11)/(0.1)`

`x \leq 110`

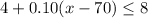
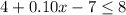
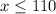
For a monthly cost of at most $8, you need to have at most 110 calling minutes.

For a monthly cost of at least $7 and at most $8, you can have between 100 and 110 calling minutes.