Question

A myopic person (assume no astigmatism) is diagnosed with a far point of 160 cm. What corrective prescription should they be supplied to enable the person to see objects in the distance?

Answer 1

- 1.428 D

Step-by-step explanation:

A myopic person is able to see the nearby objects clearly but cannot see the far off objects very clearly. It can be cured by using concave lens of suitable power.

far point = 70 cm

v = - 70 cm (position of image from the lens)

u = ∞ (position of object from lens)

Let f be the focal length of the lens

Use lens equation

`(1)/(f)=(1)/(v)-(1)/(u)`

`(1)/(f)=(1)/(-70)-(1)/(∞)`

f = - 70 cm

`P=(1)/(f)`

Where, P is the power of lens

P = - 1.428 Dioptre

Thus, the power of lens used is - 1.428 D.

Answer 2

The person should use a convex lens of power -0.625 D.

Step-by-step explanation:

Given that, the far point of the person, with myopic eye, is 160 cm.

It means that the image of an object, which is at infinity, is formed at this point 160 cm distance away from the person's eye.

If the object is infinity, then the object distance, u = -
`\infty`.

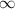Image distance, v = -160 cm.

u and v are taken to be negative because the object and the image of the object are on the side of the eye from where the light is coming.

Let the focal length of the lens which is to be used for the correction of this myopic eye be f, then using lens equation,

`\rm \frac 1f = \frac 1v-\frac 1u=\frac 1{-160 }-\frac1{-\infty}=\frac 1{-160}-0=\frac 1{-160}.\\\Rightarrow f=-160\ cm.`

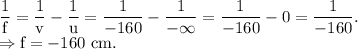
The negative focal length indicates that the lens should be convex.

The power of the lens is given by

`\rm P=(1)/(f)=(1)/(-160\ cm )=(1)/(-1.6\ m)=-0.625\ D.`

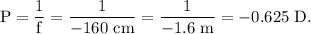
So, the person should use a convex lens of power -0.625 D.