Explanation:
Proposition If a, b

 , then
, then
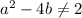
You can prove this proposition by contradiction, you assume that the statement is not true, and then show that the consequences of this are not possible.
Suppose the proposition If a, b

 , then
, then
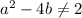 is false. Thus there exist integers If a, b
is false. Thus there exist integers If a, b

 for which
for which
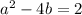
From this equation you get
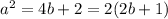 so
so
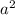 is even. Since
is even. Since
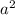 is even, a is even, this means
is even, a is even, this means
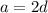 for some integer d. Next put
for some integer d. Next put
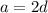 into
into
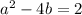 . You get
. You get
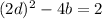 so
so
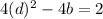 . Dividing by 2, you get
. Dividing by 2, you get
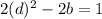 . Therefore
. Therefore
 , and since
, and since
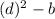

 , it follows that 1 is even.
, it follows that 1 is even.
And that is the contradiction because 1 is not even. In other words, we were wrong to assume the proposition was false. Thus the proposition is true.