Answer:
8 is the modular inverse of 12 mod 19 since 12*8 mod 19 ≡ 1.
Explanation:
We need to find the inverse of 12 modulo 19.
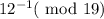
If a is an integer and m is modulo, then the modular multiplicative inverse of a modulo m is an integer b such that
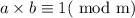
Substitute different values of b and check whether that remainder is 1 after modulo 19.
At b=1,
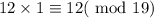
At b=2,

At b=3,
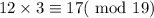
At b=4,
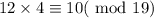
At b=5,
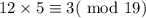
At b=6,
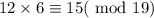
At b=7,
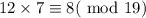
At b=8,
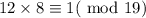
Therefore, 8 is the modular inverse of 12 mod 19 since 12*8 mod 19 ≡ 1.