Answer:
Height of oil is 7.06 meters.
Step-by-step explanation:
The situation is shown in the attached figure
The pressure at the bottom of the tank as calculated by equation of static pressure distribution is given by
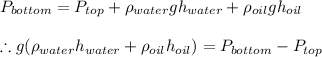
Applying the given values we get
