Question

Find the wavelength in meters for a transverse mechanical wave with an amplitude of 10 cm and a radian frequency of 20π rad/s if the medium through which it travels has a bulk modulus of 40 MPa and a density of 1000 kg/m^3.

Answer 1

The wavelength of the wave is 20 m.

Step-by-step explanation:

Given that,

Amplitude = 10 cm

Radial frequency
`\omega = 20\pi\ rad/s`

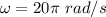
Bulk modulus = 40 MPa

Density = 1000 kg/m³

We need to calculate the velocity of the wave in the medium

Using formula of velocity

`v=\sqrt{(k)/(\rho)}`

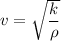
Put the value into the formula

`v=\sqrt{(40*10^(6))/(10^3)}`

`v=200\ m/s`

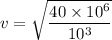
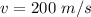
We need to calculate the wavelength

Using formula of wavelength

`\lambda =(v)/(f)`

`\lambda=(v*2\pi)/(\omega)`

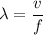
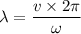
Put the value into the formula

`\lambda=(200*2\pi)/(20\pi)`

`\lambda=20\ m`

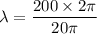
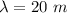
Hence, The wavelength of the wave is 20 m.