Question

A student walks (2.9±0.1)m, stops and then walks another (3.9 ±0.2)m in the same directionWith the given uncertainties, what is the smallest distance the student could possibly be from the starting point?

Answer 1

The smallest distance the student that the student could be possibly be from the starting point is 6.5 meters.

Step-by-step explanation:

For 2 quantities A and B represented as

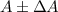`A\pm \Delta A` and
`B\pm \Delta B`

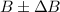
The sum is represented as

`Sum=(A+B)\pm (\Delta A+\Delta B)`

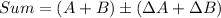
For the the values given to us the sum is calculated as

`Sum=(2.9+3.9)\pm (0.1+0.2)`

`Sum=6.8\pm 0.3`

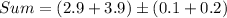
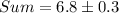
Now the since the uncertainity inthe sum is
`\pm 0.3`

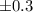
The closest possible distance at which the student can be is obtained by taking the negative sign in the uncertainity

Thus closest distance equals
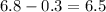`6.8-0.3=6.5`meters