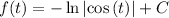Question

Find the solution of cos(t) * f ` (t) = sin(t)

Answer 1

The solution is
`f(t)=-\ln \left|\cos \left(t\right)\right|+C`

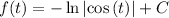
Explanation:

We know that this ordinary differential equation (ODE) is separable if we can write F(x,y) = f(x)g(y) for some function f(x), g(x).

We can write this ODE in this way

`cos(t) \cdot f'(t)=sin(t)\\f'(t)=(sin(t))/(cos(t))`

`\mathrm{If\quad }f^(') \left(x\right)=g\left(x\right)\mathrm{\quad then\quad }f\left(x\right)=\int g\left(x\right)dx`

`f(t) =\int\limits{(sin(t))/(cos(t))} \, dt`

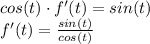
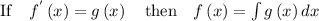
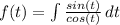
To solve this integral we need to follow this steps

`\int (\sin \left(t\right))/(\cos \left(t\right))dt = \\\mathrm{Apply\:u-substitution:}\:u=\cos \left(t\right)\\\int (\sin \left(t\right))/(u)dt \\\mathrm{And \:du=-sin(t)\cdot dt}\\\mathrm{so \>dt=(du)/(-sin(t))}\\\int (\sin \left(t\right))/(u)dt = -\int (1)/(u)du`

`\mathrm{Use\:the\:common\:integral}:\quad \int (1)/(u)du=\ln \left(\left|u\right|\right)\\-ln|u|\\\mathrm{Substitute\:back}\:u=\cos \left(t\right)\\-\ln \left|\cos \left(t\right)\right|\\`

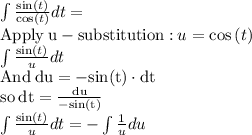
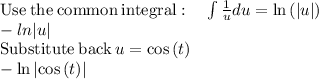
Add the constant of integration

`f(t)=-\ln \left|\cos \left(t\right)\right|+C`