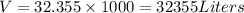Question

A storage tank, used in a fermentation process, is to be rotationally molded from polyethylene plastic. This tank will have a conical section at the bottom, right circular cylindrical mid-section and a hemispherical dome to cover the top. The radius of the tank is 1.5 m, the cylindrical side-walls will be 4.0 m in height, and the apex of the conic section at the bottom has an included angle of 60°. If the tank is filled to the top of the cylindrical side-walls, what is the tank capacity in liters?

Answer 1

The volume up to cylindrical portion is approx 32355 liters.

Step-by-step explanation:

The tank is shown in the attached figure below

The volume of the whole tank is is sum of the following volumes

1) Hemisphere top

Volume of hemispherical top of radius 'r' is

`V_(hem)=(2)/(3)\pi r^3`

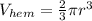
2) Cylindrical Middle section

Volume of cylindrical middle portion of radius 'r' and height 'h'

`V_(cyl)=\pi r^2\cdot h`

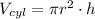
3) Conical bottom

Volume of conical bottom of radius'r' and angle
`\theta` is

`V_(cone)=(1)/(3)\pi r^3* (1)/(tan((\theta )/(2)))`

Applying the given values we obtain the volume of the container up to cylinder is

`V=\pi 1.5^2* 4.0+(1)/(3)* (\pi 1.5^(3))/(tan30)=32.355m^(3)`

Hence the capacity in liters is
`V=32.355* 1000=32355Liters`