Question

A basic cellular phone plan costs $30 per month for 50 calling minutes. Additional time costs $0.50 per minute. The formula C 30 +0.50(x - 50) gives the monthly cost for this plan, C, for x calling minutes, where x>50. How many calling minutes are possible for a monthly cost of at least $35 and at most $40? For a monthly cost of at least $35 and at most $40 sxs calling minutes are possible S

Answer 1

Explanation:

Given that a basic cellular phone plan costs $30 per month for 50 calling minutes

i.e. C(x) =
`30+0.50(x-50)`, where x = calling minutes

Here 30 is fixed upto 50 calls after that cost increases at 0.50 per minute talk time.

`C(x) = 30+0.5x-25 = 0.5x+5\\`

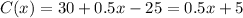
When monthly cost is atleast 35 and atmost 40 we have

`35\leq C(x)\leq 40\\35\leq 0.5x+5\leq 40\\30\leq 0.5x\leq 35\\60\leq x\leq 70`

i.e. talking time must be atleast 60 minutes and atmost 70 minutes