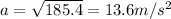Question

From a crouched position an excellent human jumper launches herself upwards. The jumpers full height is 168 cm, but in the crouched position her height is half of that value. The jumper accelerates from the crouched position until she reaches her full height. Her motion then carries her upward until her center of mass is 90 cm above its position when she is standing. At what velocity must the jumper leave the ground to reach this height? What constant acceleration must be maintained to reach this initial velocity? Assuming a constant acceleration, how long in seconds does it take to accelerate from rest to this initial velocity?

Answer 1

a) 4.2 m/s

b) 13.6 m/s^2

Step-by-step explanation:

She is jumping, and when her feet no longer touch the ground she is in free fall, only affected by the acceleration of gravity.

The equation for position under constant acceleration is:

Y(t) = Y0 + Vy0 * t + 1/2 * a * t^2

We set up a reference system that has its origin at the point her center of mass is when she is standing and the positive Y axis points upwards, then:

Y0 = 0 m

a = -9.81 m/s^2

The equation for speed under constant acceleration is:

V(t) = Vy0 + a * t

We know that when she reaches her highes point her vertical speed will be zero because that is wehn her movement changes direction. We'll call this moment t1.

0 = Vy0 + a * t1

a * t1 = -Vy0

t1 = -Vy0/a

If we replace this value on the position equation we can find her initial speed:

Y(t1) = Y0 - Vy0 * Vy0/a + 1/2 * a * (-Vy0/a)^2

Y(t1) = - Vy0^2/a + 1/2 * Vy0^2/a

Y(t1) = -1/2 * Vy0^2 / a

Vy0^2 = -2 * a * Y(t1)

`Vy0 = √(-2 * a * Y(t1))`

`Vy0 = √(-2 * (-9.81) * 0.9) = 4.2 m/s`

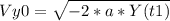
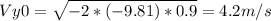
I assume her center of mass is at half her height, so when she is standing it would be at 93 cm of the grouind, and when she is crouching at 46.5 cm.

Therefore when she jumps her centr of mass moves 0.465 m before leaving the ground.

During that trajectory she moves with acceleration.

Y(t) = Y0 + Vy0 * t + 1/2 * a *t^2

In this case her initial position is

Y0 = -0.465

Her initial speed is

Vy0 = 0

At t=t0 her position will be zero

The equation for speed under constan acceleration is

Vy(t) = Vy0 + a * t

Her speed at t0 will be 4.2 m/s

4.2 = a * t0

t0 = 4.2 / a

0 = -0.465 - 1/2 * 9.81 * (4.2 / a)^2

0.465 = 4.9 * 17.6 / a^2

a^2 = 86.2 / 0.465

`a = √(185.4) = 13.6 m/s^2`