Question

An election forecasting model has a 50:50 chance of correctly predicting the election winner when there are two candidates. Before seeing the prediction of the model an election researcher estimates that there is a 75% chance that candidate Allan will defeat candidate Barnes. She then finds out that the model has predicted a victory for Barnes. Her posterior probability of a victory for Allan should be: (a) (b) (c) (d) 0.375 0.500 0.750 1.000

Answer 1

Te correct answer is c) 0.750

Explanation:

Lets call:

A = {Allan wins the election}

B = {Barnes wins the election}

MA = {the model predicts that Allan wins}

MB = {the model predicts Barnes wins}

We know that the model has a 50:50 chance of correctly predicting the election winner when there are two candidates. Then:

P(MA | A) = 0.5 = P(MA | B)

P(MB | B) = 0.5 = P(MB | A)

The prior probability P(A) given by the election researcher is 0.75

We must find the posterior probability P(A | MB)

We use Bayes theorem:

`P(A|MB) = (P(MB|A)P(A))/(P(MB)) = (0.5*0.75)/(0.5) = 0.75`

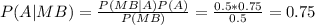
We used the result:

`P(MB) = P(MB|A)P(A) + P(MB|B)P(B) = 0.5*0.75+0.5*0.25=0.5`