Answer: 374416
Explanation:
Given : A test requires that you answer first Part A and then either Part B or Part C.
Part A consists of 4 true false questions, Part B consists of 6 multiple-choice questions with one correct answer out of five, and Part C consists of 5 multiple-choice questions with one correct answer out of six.
i.e. 2 ways to answer each question in Part A.
For 4 questions, Number of ways to answer Part A =
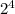
5 ways to answer each question in Part B.
For 6 questions, Number of ways to answer Part B =

6 ways to answer each question in Part C.
For 5 questions, Number of ways to answer Part C =
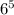
Now, the number of ways to completed answer sheets are possible :_

Hence, the number of ways to completed answer sheets are possible = 374416