Question

At an effective annual interest rate of i > 0, each of the following two sets of payments has present value K: (i) A payment of 169 immediately and another payment of 169 at the end of two years. (ii) A payment of 225 at the end of two years and another payment of 225 at the end of four years. Calculate K.

Answer 1

The present value of K is,
`K=251.35`

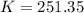
Explanation:

Hi

First of all, we need to construct an equation system, so

`(1)K=(169)/((1+i)) +(169)/((1+i)^(2))`

`(2)K=(225)/((1+i)^(2)) +(225)/((1+i)^(4))`

Then we equalize both of them so we can find
`i`

`(3)(169)/((1+i)) +(169)/((1+i)^(2))=(225)/((1+i)^(2)) +(225)/((1+i)^(4))`

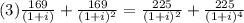
To solve it we can multiply
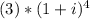`(3)*(1+i)^(4)` to obtain
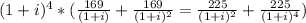`(1+i)^(4)*((169)/((1+i)) +(169)/((1+i)^(2))=(225)/((1+i)^(2)) +(225)/((1+i)^(4)))`, then we have
`225(1+i)^(2)+225=169(1+i)^(3)+169(1+i)^(2)`.

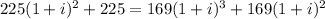This leads to a third-grade polynomial
`169i^(3)+451i^(2)+395i-112=0`, after computing this expression, we find only one real root
`i=0.2224`.

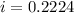Finally, we replace it in (1) or (2), let's do it in (1)
`K=(169)/((1+0.2224)) +(169)/((1+0.2224)^(2))\\\\K=251.35`