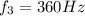Question

James is running toward the base of a tall canyon wall at 2 m/s while screaming at 355 Hz. The wind is blowing the opposite direction at 3 m/s. What beat frequency does he hear from his own echo off the wall? Use 350 m/s for the speed of sound.

Answer 1

`f_(ecco)  = 360 Hz`

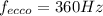
Step-by-step explanation:

The change of frecuency of sound due to the movement of the source is colled Doppler Effect.

As James (the source) is running toward the wall, the frecuency reaching the wall (so the eco sound) will be higher than the source. In this case the frecuency at the wall will be:

`f_(2)  = f_(1)  ((v)/(v-v_(s) ) )`

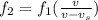
where
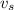`v_(s)` is the speed of source, 2 m/s

and
`v` is the speed of sound, given that we have wind movind the air in the opposite direction respect to the wall, the speed of sound would be:

`v = 350 (m)/(s) - 3 (m)/(s) = 347 (m)/(s)`

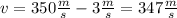
Replacing the values:
`f_(2)  = 357 Hz`

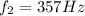
Now the wall becames the new source, and James (the observer is aproaching the source), for an observer aproaching the source the new frecuency will be:

`f_(3)  = f_(2)  (1 + (v_(s))/(v) )`

Now the waves are traveling in the direction of wind, so the velocity of sound will be:

`v = 350 (m)/(s) + 3 (m)/(s) = 353 (m)/(s)`

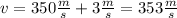
Replacing:

`f_(3)  = 360 Hz`