Question

The velocity of a point mass that moves along the s-axis is given by s' = 40 - 3t^2 m/s, where t is in seconds. Find displacement of the particle from t = 2 s to t 6 s.

Answer 1

The displacement is -48m.

Step-by-step explanation:

Velocity is the rate of change of displacement. So, the instantaneous displacement is calculated by the integration of velocity function with respect to time. Displacement in range of time is calculated by integrating the velocity function with respect to time with in time range.

Given:

Velocity along the s-axis is

`s{}'=40-3t^(2)`

time range is t=2s to t=6s.

Calculation:

Step1

Displacement in the time range t=2s to t=6s is calculated as follows:

`\frac{\mathrm{d}s}{\mathrm{d}t}=40-3t^(2)`

`ds=(40-3t^(2))dt`

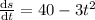
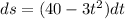
Step2

Integrate the above equation with respect to time with the lower limit as 2 and upper limit as 6 as follows:

`\int ds=\int_(2)^(6)(40-3t^(2))dt`

`s=(40*6-40*2)-3((1)/(3))(6^(3)-2^(3))`

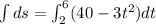
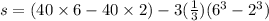
s=160-208

s=-48m

Thus, the displacement is -48m.