Answer: 100
Explanation:
Given : The lodhl diner offers a meal combination consisting of an appetizer, a soup, a main course, and a dessert.
There are 5 appetizers, 5 soups, 4 main courses, and 5 desserts.
Also, a dessert and a appetizer are not allowed to take together.
By Fundamental counting principal ,
Number of three-course meals with dessert and without appetizer :
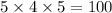 (1)
(1)
Number of three-course meals with appetizer and without dessert :
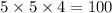 (2)
(2)
Now, the number of meals with either dessert or appetizer :-
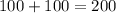 [Add (1) and (2)]
[Add (1) and (2)]