Question

The position of a particle moving along a straight line is defined by the relation. s = t^3 – 6t^2 – 15t + 40, where s is expressed in feet and t in seconds. Determine:(a) s when t = 3 seconds.(b) v when t = 5 seconds. (c) a when t = 4 seconds.(d) the time when the velocity is equal to zero. What is important about this information?

Answer 1

1) s(3) = -32 feet.

2)v(5) = 3 feet/sec

3)a(4) = 12
`feet/s^(2)`

4) Velocity becomes zero at t = 5 seconds

Step-by-step explanation:

Given that position as a function of time is

`s(t)=t^(3)-6t^(2)-15t+40`

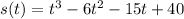
Now by definition of velocity we have

`v=(ds)/(dt)\\\\v=(d)/(dt)(t^(3)-6t^(2)-15t+40)\\\\\therefore v(t)=3t^(2)-12t-15`

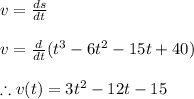
Now by definition of acceleration we have

`a=(dv)/(dt)\\\\a=(d)/(dt)(3t^(2)-12t-15)\\\\\therefore a(t)=6t-12`

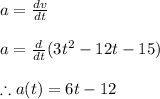
Applying values of time in corresponding equations we get

1) s(3)=
`3^(3)-6* (3)^(2)-15* 3+40=-32feet`

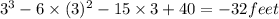
2)v(5)=
`3* {5}^(2)-12* 5-15=3feet/sec`

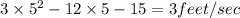
3)a(4)=
`6* 4-12=12ft/s^(2)`

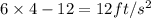
4)To obatin the time at which velocity is zero equate the velocity function with zero we get

`3t^(2)-12t-15=0\\\\t^(2)-4t-5=0\\\\t^(2)-5t+t-5=0\\\\t(t-5)+1(t-5)=0\\\\(t-5)(t+1)=0\\\\\therefore t=5\\\\or\\\therefore t=-1`

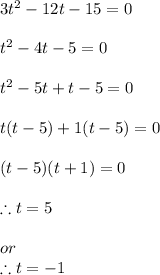
Thus the correct time is 5 seconds at which velocity becomes zero.