Question

The tallest living man at one time had a height of 230 cm. The shortest living man at that time had a height of 91.3 cm. Heights of men at that time had a mean of 170.53 cm and a standard deviation of 5.91 cm. Which of these two men had the height that was more​ extreme?

Answer 1

Answer: The shortest living man at that time had the height that was more​ extreme.

Explanation:

We will z scores to solve this exercise. The formula we need is:

`z=(x-\mu)/(\sigma)`

Where
`x` is the raw score,
`\mu` is the mean and
`\sigma` is the standard deviation.

We know at that time heights of men had a mean of 170.53 centimeters and a standard deviation of 5.91 centimeters, then:

`\u=170.53\\\\\sigma=5.91`

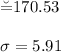
Knowing that the tallest living man at that time had a height of 230 centimeters, we get:

`z=(230-170.53)/(5.91)\approx10.07`

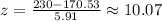
And knowing that the shortest living man at that time had a height of 91.3 centimeters, we get:

`z=(91.3-170.53)/(5.91)\approx-13.40`

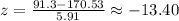
Based on this, we can conclude that the shortest living man at that time had the height that was more​ extreme.