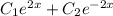Question

Find a general solution of y" – 4y = 0.

Answer 1

y =
`C_(1)e^(2x) + C_(2)e^(-2x)`

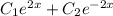
Explanation:

We are given the differential equation: y'' - 4y = 0

We have to find the general solution.

The auxiliary equation for the above differential equation can be written as:

m² - 4 = 0

We solve for m.

⇒m² = 4

⇒m = ±2

⇒
`m_(1)` = +2 and
`m_(2)` = -2

Thus, we have two distinct roots or we have two distinct values of m.

Thus, the general solution will be of the form:

y =
`C_(1)e^{m_(1)x} + C_(2)e^{m_(2)x}`

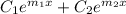
y =
`C_(1)e^(2x) + C_(2)e^(-2x)`