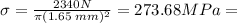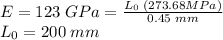Question

A cylindrical specimen of some metal alloy having an elastic modulus of 123 GPa and an original cross-sectional diameter of 3.3 mm will experience only elastic deformation when a tensile load of 2340 N is applied. Calculate the maximum length of the specimen before deformation if the maximum allowable elongation is 0.45 mm.

Answer 1

maximum length of the specimen before deformation = 200 mm

Step-by-step explanation:

Hi!

If we have a cylinder with length L₀ , and it is elasticaly deformed ΔL (so the final length is L₀ + ΔL), the strain is defined as:

`\epsilon =(\Delta L)/(L_0)`

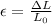
And the tensile stress is:

`\sigma = (F)/(A)\\F = \text{tensile load}\\A = \text{ cross section area}`

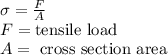
Elastic modulus E is defined as:

`E = (\sigma)/(\epsilon )`

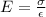
In this case ΔL = 0.45 mm and we must find maximum L₀. We know that A=π*r², r=(3.3/2) mm. Then:

`\sigma=(2340N)/(\pi (1.65 \;mm)^2)=273.68 MPa =`

`E=123\;GPa=(L_0 \;(273.68MPa))/(0.45\;mm ) \\ L_0 = 200\; mm`