Answer:
1) False 2) True 3) True 4) True
Explanation:
1)FALSE
We can prove this by giving a counterexample,
Take the arithmetic sequence
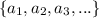
where
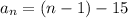
in this case d=1
Then

2)TRUE
Given that for an arithmetic sequence
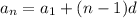
Where d is a constant other than 0, then
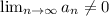
and so, the series
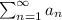
diverges.
3)TRUE
This is the definition of infinite sum.
If
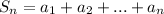
then
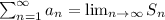
4)TRUE
If
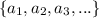
is a geometric sequence, then the n-th partial sum is given by
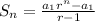
Since r<1
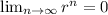
and so, the geometric series
