Question

An airplane undergoes the following displacements: First, it flies 40 km in a direction 30° east of north. Next, it flies 56 km due south. Finally, it flies 100 km 30° north of west. Using analytical methods, determine how far the airplane ends up from its starting point.

Answer 1

The airplane ends up approximately 72.53 km from its starting point.

Step-by-step explanation:

To determine how far the airplane ends up from its starting point after these displacements, we can use vector addition to find the resultant displacement. Since the movements are given in terms of directions relative to north, we can use a coordinate system where north corresponds to the positive y-axis, and east corresponds to the positive x-axis.

Let's start with the first displacement:
1. The airplane flies 40 km in a direction 30° east of north.
We can resolve this displacement into x and y components:
- The x-component (eastward) is 40 km * sin(30°) because the angle is measured from the north (y-axis).
- The y-component (northward) is 40 km * cos(30°) because the angle is with respect to the vertical (north direction).

Using the fact that sin(30°) = 1/2 and cos(30°) = √3/2:
- x1 = 40 km * 1/2 = 20 km
- y1 = 40 km * √3/2 ≈ 40 km * 0.866 = 34.64 km

Now for the second displacement:
2. The airplane flies 56 km due south.
This movement is along the negative y-axis.
- x2 = 0 km (no movement east or west)
- y2 = -56 km (southward)

For the third displacement:
3. The airplane flies 100 km 30° north of west.
- The x-component (westward) will be -100 km * cos(30°) because we are measuring the angle from the north and going west is negative in our coordinate system.
- The y-component (northward) will be 100 km * sin(30°).

Using the trigonometric values found earlier:
- x3 = -100 km * √3/2 ≈ -100 km * 0.866 = -86.6 km
- y3 = 100 km * 1/2 = 50 km

Having found the components for each displacement, we can now sum them up to find the total displacement.

Total x-component (x_total) = x1 + x2 + x3 = 20 km + 0 km - 86.6 km = -66.6 km (westward)
Total y-component (y_total) = y1 + y2 + y3 = 34.64 km - 56 km + 50 km = 28.64 km (northward)

Now, we can determine the magnitude of the resultant displacement vector using the Pythagorean theorem:

R = √(x_total^2 + y_total^2)
R = √((-66.6 km)^2 + (28.64 km)^2)
R = √(4440.96 km^2 + 820.5696 km^2)
R = √(5261.5296 km^2)
R ≈ 72.53 km

So, the airplane ends up approximately 72.53 km from its starting point.

Answer 2

Distance from start point is 72.5km

Step-by-step explanation:

The attached Figure shows the plane trajectories from start point (0,0) to (x1,y1) (d1=40km), then going from (x1,y1) to (x2,y2) (d2=56km), then from (x2,y2) to (x3,y3) (d3=100). Taking into account the angles and triangles formed (shown in the Figure), it can be said:

`x1=d1*cos(60), y1=d1*sin(60)\\\\ x2=x1 , y2=y1-d2\\\\ x3=x2-d3*cos(30) , y3=y2+d3*sin(30)`

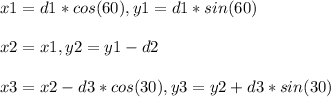
Using the Pitagoras theorem, the distance from (x3,y3) to the start point can be calculated as:

`d=\sqrt{x3^(2) +y3^(2) }`

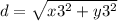
Replacing the given values in the equations, the distance is calculated.