Question

A Coca Cola can with diameter 62 mm and wall thickness 300 um has an internal pressure of 100 kPa. Calculate the principal stresses at a point on the cylindrical surface of the can far from its ends.

Answer 1

`\sigma _1=10.33MPa`

`\sigma _2=5.16MPa`

Step-by-step explanation:

Given that

Diameter(d)=62 mm

Thickness(t)= 300 μm=0.3 mm

Internal pressure(P)=100 KPa

Actually there is no any shear stress so normal stress will become principle stress.This is the case of thin cylinder.The stress in thin cylinder are hoop stress and longitudinal stress .

The hoop stress

`\sigma _h=(Pd)/(2t)`

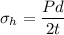
Longitudinal stress

`\sigma _l=(Pd)/(4t)`

Now by putting the values

`\sigma _h=(Pd)/(2t)`

`\sigma _h=(100* 62)/(2* 0.3)`

`\sigma _h=10.33MPa`

`\sigma _l=5.16MPa`

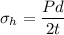
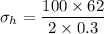
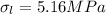
So the principle stress are

`\sigma _1=10.33MPa`

`\sigma _2=5.16MPa`