Question

A model rocket rises with constant acceleration to a height of 3.1 m, at which point its speed is 28.0 m/s. a. How much time does it take for the rocket to reach this height?

b. What was the magnitude of the rocket's acceleration?
c. Find the height of the rocket 0.10 s after launch.
d. Find the speed of the rocket 0.10 s after launch.

Answer 1

Step-by-step explanation:

It is given that,

Height, h = 3.1 m

Initial speed of the rocket, u = 0

Final speed of the rocket, v = 28 m/s

(b) Let a is the acceleration of the rocket. Using the formula as :

`a=(v^2-u^2)/(2h)`

`a=((28)^2)/(2* 3.1)`

`a=126.45\ m/s^2`

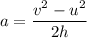
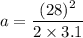
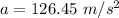
(a) Let t is the time taken to reach by the rocket to reach to a height of h. So,

`t=(v-u)/(a)`

`t=(28\ m/s)/(126.45\ m/s^2)`

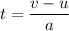
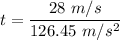
t = 0.22 seconds

(c) At t = 0.1 seconds, height of the rocket is given by :

`h=ut+(1)/(2)at^2`

`h=(1)/(2)* 126.45* (0.1)^2`

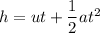
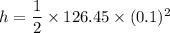
h = 0.63 meters

(d) Let v' is the speed of the rocket 0.10 s after launch.

So,
`v'=u+at`

`v'=0+126.45* 0.1`

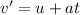
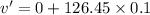
v' = 12.64 m/s

Hence, this is the required solution.