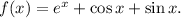Question

Find the inverse Laplace transforms, as a function of x, of the following functions:

2s^2/ (s – 1)(s^2 +1)

Answer 1

Answer: The required answer is

`f(x)=e^x+\cos x+\sin x.`

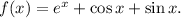
Step-by-step explanation: We are given to find the inverse Laplace transform of the following function as a function of x :

`F(s)=(2s^2)/((s-1)(s^2+1)).`

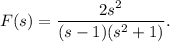
We will be using the following formulas of inverse Laplace transform :

`(i)~L^(-1)\{(1)/(s-a)\}=e^(ax),\\\\\\(ii)~L^(-1)\{(s)/(s^2+a^2)\}=\cos ax,\\\\\\(iii)~L^(-1)\{(1)/(s^2+a^2)\}=(1)/(a)\sin ax.`

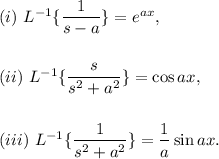
By partial fractions, we have

`(s^2)/((s-1)(s^2+1))=(A)/(s-1)+(Bs+C)/(s^2+1),`

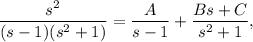
where A, B and C are constants.

Multiplying both sides of the above equation by the denominator of the left hand side, we get

`2s^2=A(s^2+1)+(Bs+C)(s-1).`

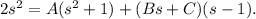
If s = 1, we get

`2* 1=A(1+1)\\\\\Rightarrow A=1.`

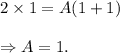
Also,

`2s^2=A(s^2+1)+(Bs^2-Bs+Cs-C)\\\\\Rightarrow 2s^2=(A+B)s^2+(-B+C)s+(A-C).`

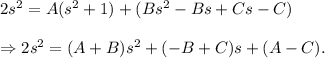
Comparing the coefficients of x² and 1, we get

`A+B=2\\\\\Rightarrow B=2-1=1,\\\\\\A-C=0\\\\\Rightarrow C=A=1.`

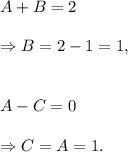
So, we can write

`(2s^2)/((s-1)(s^2+1))=(1)/(s-1)+(s+1)/(s^2+1)\\\\\\\Rightarrow (2s^2)/((s-1)(s^2+1))=(1)/(s-1)+(s)/(s^2+1)+(1)/(s^2+1).`

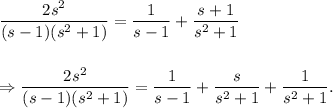
Taking inverse Laplace transform on both sides of the above, we get

`L^(-1)\{(2s^2)/((s-1)(s^2+1))\}=L^(-1)\{(1)/(s-1)\}+L^(-1)\{(s)/(s^2+1)+(1)/(s^2+1)\}\\\\\\\Rightarrow f(x)=e^(1* x)+\cos (1* x)+(1)/(1)\sin(1* x)\\\\\\\Rightarrow f(x)=e^x+\cos x+\sin x.`

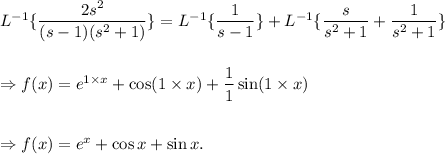
Thus, the required answer is

`f(x)=e^x+\cos x+\sin x.`