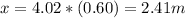Question

In a game of basketball, a forward makes a bounce pass to the center. The ball is thrown with an initial speed of 4.4 m/s at an angle of 24° above the horizontal. It is released 0.70 m above the floor. Q1: What horizontal distance does the ball cover before bouncing? please show how to solve for t in the problem.

Answer 1

The horizontal distance is 2.41 mts

Step-by-step explanation:

For this problem, we will use the formulas of parabolic motion.

`Y=Yo+Voy*t+(1)/(2)*a*t^2\\Vx=V*cos(\alpha)\\Vy=V*sin(\alpha)`

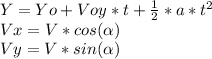
We need to find the time of the whole movement (t), for that we will use the first formula:

we need the initial velocity for that:

`Vy=4.4*sin(24^o)\\Vy=1.79m/s`

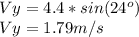
so:

`0=0.70+1.79*t+(1)/(2)*(-9.8)*t^2`

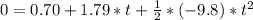
now we have a quadratic function, solving this we obtain two values of time:

t1=0.60sec

t2=-0.234sec

the obvious value is 0.60sec, we cannot use a negative time.

Now we are focusing on finding the horizontal distance.

the movement on X is a constant velocity motion, so:

`x=Vx*t`

`Vx=4.4*cos(24^o)=4.02m/s\\`

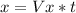
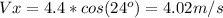
so:

`x=4.02*(0.60)=2.41m`