Answer:
6.328m/s
Step-by-step explanation:
We can solve this problem using conservation of energy. The sum of the potential and kinetic energy at point A must be equal to the sum of the potential and kinetic energy at point N.
The potential energy of the particle is equal to the electric potential times the charge of the particle.
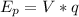
The kinetic energy is half the mass times velocity squared:
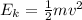
So, the energy at point A and B is:
