Question

Prove that the square of any even number is always a multiple of 4.

Answer 1

Answer and Explanation:

To prove : The square of any even number is always a multiple of 4.

Proof :

The even numbers is defined as number end with 0,2,4,6,8 or the even number are multiple of 2.

Let the general even number be '2n'.

Squaring the number
`(2n)^2=2^2* n^2`

`(2n)^2=4n^2`

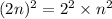
As 4 is the multiple of n².

So, If we square any even number it is always a multiple of 4.

For example,

`2^2=4=4* 1\\4^2=16=4* 4\\6^2=36=4* 9\\8^2=64=4* 16`

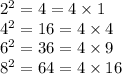
Hence proved.