Question

An airplane left airport A flying on a course of 72 degrees.

After flying 495 km, the plane was just able to pick up
communication signals from airport B which is due east of airport
A. If airport B's communication signals can be picked up within a
radius of 300 km from airport B, for how many kilometers can the
airplane fly and still be in contact with airport B? Give you
answer to one decimal place.

Answer 1

Distance for which Aeroplane can be in contact with Airport B is = 396.34 km

Explanation:

In the question,

We have an Airport at point A and another at point B.

Now,

Airplane flying at the angle of 72° with vertical catches signals from point D.

Distance travelled by Airplane, AD = 495 km

Now, Let us say,

AB = x

So,

In triangle ABD, Using Cosine Rule, we get,

`cos(90-72) =cos18= (AB^(2)+AD^(2)-BD^(2))/(2.AD.AB)`

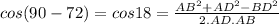
So,

On putting the values, we get,

`cos18 = (x^(2)+495^(2)-300^(2))/(2(495)(x))\\0.951(990x)=x^(2)+245025-90000\\x^(2)-941.54x+155025=0\\`

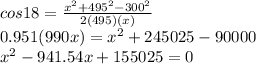
Therefore, x is given by,

x = 212.696, 728.844

So,

The value of x can not be 212.696 as the length of LB (radius) itself is 300 km.

So,

x = 728.844 km

So,

AL = AB - BL

AL = x - 300

AL = 728.844 - 300

AL = 428.844 km

Now, in the circle from a property of secants we can say that,

AL x AM = AD x AC

So,

428.844 x (728.844 + 300) = 495 x AC

441213.576 = 495 x AC

AC = 891.34 km

So,

The value of CD is given by,

CD = AC - AD

CD = 891.34 - 495

CD = 396.34 km

Therefore, the distance for which the Aeroplane can still be in the contact with Airport B is 396.34 km.