Answer: The required distance between the points between A(1, 1) and B(7, −7) is 10 units.
Step-by-step explanation: We are given to explain the distance formula. Also, to calculate the distance between A(1, 1) and B(7, −7).
Distance formula : The distance between any two two points with co-ordinates (a, b) and (c, d) is given by
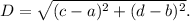
Therefore, the distance between the points A(1, 1) and B(7, −7) is given by
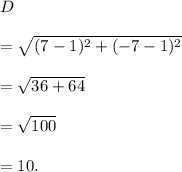
Thus, the required distance between the points between A(1, 1) and B(7, −7) is 10 units.