Question

Is (-2,-1) , (1,-4) and (5,-3) , (-2,-8) perpendicular?

Answer 1

keeping in mind that perpendicular lines have negative reciprocal slopes, let's find the slopes of these two, if they're indeed perpendicular, they'll be negative reciprocal of each other, meaning one slope will be the same as the other, but negative and upside-down, and thus their product will just be -1.

`\bf (\stackrel{x_1}{-2}~,~\stackrel{y_1}{-1})\qquad (\stackrel{x_2}{1}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-4}-\stackrel{y1}{(-1)}}}{\underset{run} {\underset{x_2}{1}-\underset{x_1}{(-2)}}}\implies \cfrac{-4+1}{1+2}\implies \cfrac{-3}{3}\implies \boxed{-1} \\\\[-0.35em] ~\dotfill`

`\bf (\stackrel{x_1}{5}~,~\stackrel{y_1}{-3})\qquad (\stackrel{x_2}{-2}~,~\stackrel{y_2}{-8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-8}-\stackrel{y1}{(-3)}}}{\underset{run} {\underset{x_2}{-2}-\underset{x_1}{5}}}\implies \cfrac{-8+3}{-7}\implies \cfrac{-5}{-7}\implies \boxed{\cfrac{5}{7}}`

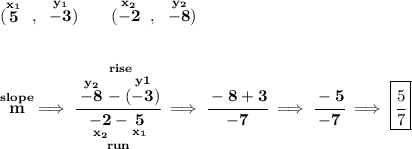
well, 5/7 is not the negative reciprocal of -1.