Answer:
If
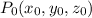 is a point on the surface, then the cartesian equation of the tangent plane at
is a point on the surface, then the cartesian equation of the tangent plane at
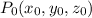 is
is
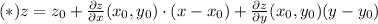 ,
,
where
 .
.
Given that
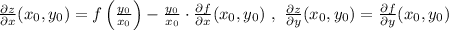 , then
, then
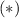 becomes
becomes
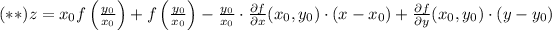 .
.
Finally, replacing
 in
in
 you have that the equality is true for all
you have that the equality is true for all
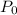 . This means that
. This means that

belongs to all tangent planes and therefore, the result follows.