Question

25% of all who enters a race do not complete. 30 haveentered.

what is the probability that exactly 5 are unable tocomplete the
race?

Answer 1

The probability that exactly 5 are unable to complete the race is 0.1047

Explanation:

We are given that 25% of all who enters a race do not complete.

30 have entered.

what is the probability that exactly 5 are unable to complete the race?

So, We will use binomial

Formula :
`P(X=r) =^nC_r p^r q^(n-r)`

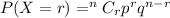
p is the probability of success i.e. 25% = 0.25

q is the probability of failure = 1- p = 1-0.25 = 0.75

We are supposed to find the probability that exactly 5 are unable to complete the race

n = 30

r = 5

`P(X=5) =^(30)C_5 (0.25)^5 (0.75)^(30-5)`

`P(X=5) =(30!)/(5!(30-5)!) *(0.25)^5 (0.75)^(30-5)`

`P(X=5) =0.1047`

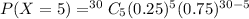
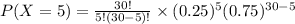
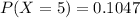
Hence the probability that exactly 5 are unable to complete the race is 0.1047