Answer: option (C)
Step-by-step explanation: The slope of a linear function is undetermined when the line is parallel respect to the y-axis. In the current problem there is no way to observe such geometrical issue, but if we consider how to derive the slope using the following expression;
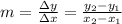 .
.
With the previous equation, we have
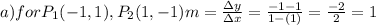 , therefore the slope is defined
, therefore the slope is defined
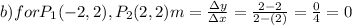 , therefore the slope is defined
, therefore the slope is defined

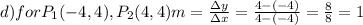
In this case, the option (C) shows that is not possible to divide over zero. Given such issue, the slope is undetermined and therefore it is a vertical line parallel to y-axis.