Answer : The change in entropy is 6 J/K
Explanation :
To calculate the change in entropy we use the formula:
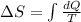
and,
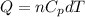
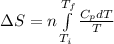
where,
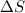 = change in entropy
= change in entropy
n = number of moles = 2 moles
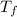 = final temperature = 303 K
= final temperature = 303 K
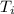 = initial temperature = 273 K
= initial temperature = 273 K
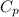 = heat capacity at constant pressure =
= heat capacity at constant pressure =
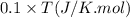
Now put all the given values in the above formula, we get:
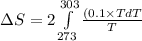
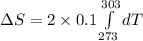
![\Delta S=2* 0.1* [T]^(303)_(273)](https://img.qammunity.org/2020/formulas/chemistry/college/614ce9nz9d7ega7chw1u4h7a45vegessuf.png)
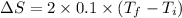
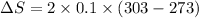
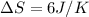
Therefore, the change in entropy is 6 J/K