Answer:

Explanation:
Given: sin x + cos x
To change the given trigonometry expression in term of sine only.
Trigonometry identity:-
Expression:
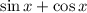
We get rid of cos x from expression and write as sine form.
Expression:

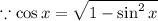
Hence, The final expression is only sine function.