Question

A satellite is launched 600 km from the surface of the earth, with an initial velocity of 8333.3 m./s, acting parallel to the tangent of the surface of the earth. Assuming the radius of the earth to be 6378 km and that is 5.976 * 10^6 kg, determine the eccentricity of the orbit.

Answer 1

eccentrcity of orbit is 0.22

Step-by-step explanation:

GIVEN DATA:

Initial velocity of satellite = 8333.3 m/s

distance from the sun is 600 km

radius of earth is 6378 km

as satellite is acting parallel to the earth therefore
`\theta angle = 0`

and radial component of given velocity is zero

we have
`h = r_o v_r_o = 6378+600 =6.97*10^6 m`

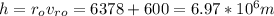
h = 6.97*10^6 *8333.3 = 58.08*10^9 m^2/s

we know that

`(1)/(r) =(GM)/(h^2) * ( i + \epsilon cos\theta)`

`GM = gr^2 = 9.81*(6.37*10^6)^2 = 398*10^(12) m^3/s`

so

`(1)/(6.97*10^6) =(398*10^(12))/((58.08*10^9)^2) * ( i + \epsilon cos0)`

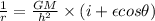
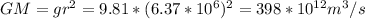
solvingt for
`\epsilon)`

`\epsilon = 0.22)`

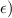
therefore eccentrcity of orbit is 0.22