Question

A random sample of 5 hinges is selected from a steady stream of product from a punch press, and the a. b. proportion nonconforming is 0.10. Sampling is with replacement. What is the probability of zero nonconforming unit in the sample? What is the probability of one nonconforming unit in the sample? hat is the probability of 2 or more nonconforming units in the sample?

Answer 1

Answer with explanation:

Given : Sample size : n= 5

The proportion nonconforming : p= 0.10

Binomial probability formula :-

`P(x)=^nC_x p^(x)(1-p)^(n-x)`

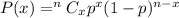
The probability of zero nonconforming unit in the sample :-

`P(0)=^5C_0 (0.10)^(0)(1-0.1)^(5)\\\\=(1)(0.9)^5\ \ [ \because\ ^nC_0=1]=0.59049`

∴ The probability of zero nonconforming unit in the sample= 0.59049

The probability of one nonconforming unit in the sample :-

`P(1)=^5C_1 (0.10)^(1)(0.9)^(4)\\\\=(5)(0.1)(0.9)^5\ \ [ \because\ ^nC_1=n]=0.295245`

∴ The probability of one nonconforming unit in the sample=0.295245

The probability of 2 or more nonconforming units in the sample :-

`P(X\geq2)=1-(P(0)+P(1))=1-(0.59049+0.295245)\\\\=1-0.885735=0.114265`

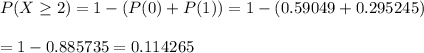
∴ The probability of 2 or more nonconforming units in the sample=0.114265