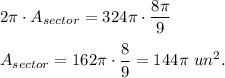Question

PLEEASSSSEEEE HHEEEEELLLLPPPPPPPP !!!!!!!!!!!!!!!!!!!!!!!!!!! Circle R is shown. Line segments Q R and S R are radii. The length of Q R is 18. Sector Q R S is shaded. The measure of central angle QRS is StartFraction 8 pi Over 9 EndFraction radians. What is the area of the shaded sector? 36Pi units squared 72Pi units squared 144Pi units squared 324Pi units squared

Answer 1

144

Explanation:

Answer 2

`144\pi\ un^2.`

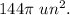
Explanation:

In the attached diagram, circle R is shown. Line segments QR and SR are radii and QR = SR = 18 units.

The measure of the central angle QRS is
`(8\pi)/(9)`

1. Find the area of the whole circle:

`A_(circle)=\pi r^2=\pi \cdot 18^2=324\pi \ un^2.`

2. Note that the whole circle is determined by the full rotation angle with measure
`2\pi` radians. So,

`\begin{array}{cc}\text{Angle}&\text{Area}\\ \\2\pi &324\pi \\ \\(8\pi )/(9)&A_(sector)\end{array}`

So, write a proportion:

`(2\pi)/((8\pi)/(9))=(324\pi)/(A_(sector))`

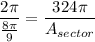
Cross multiply

`2\pi \cdot A_(sector)=324\pi \cdot (8\pi )/(9)\\ \\A_(sector)=162\pi \cdot (8)/(9)=144\pi\ un^2.`