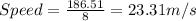Question

The position of a particle along a straight-line path is defined by s = (t3 - 6t2 - 15t + 7) ft, where t is in seconds. When t = 8 s, determine the particle’s (a) instantaneous velocity and instantaneous acceleration, (b) average velocity and average speed

Answer 1

Answer: 1) Instantaneous velocity at t= 8 equals 81m/s

2) Instantaneous acceleration at t= 8 equals
`36m/s^(2)`

3) Average velocity between 0 to 8 seconds equals 1 m/s.

4) Average speed between 0 to 8 seconds equals 23.31 m/s.

Step-by-step explanation:

Given position as a function of time as

`s(t)=t^3-6t^2-15t+7`

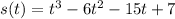
Now by definition of velocity 'v' we have

`v=(d)/(dt)\cdot s(t)\\\\v=(d)/(dt)\cdot (t^3-6t^2-15t+7)\\\\v=3t^2-12t-15`

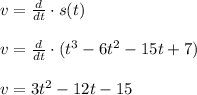
Thus velocity at t = 8 seconds equals
`v(8)=3* 8^2-12* 8-15=81m/s`

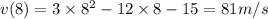
Now by definition of acceleration 'a' we have

`a=(d)/(dt)\cdot v(t)\\\\a=(d)/(dt)\cdot (3t^2-12t-15)\\\\a=6t-12`

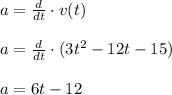
Thus acceleration at t = 8 seconds equals
`a(8)=6* 8-12=36m/s^(2)`

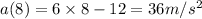
Part 2)

The average of any function is mathematically defined as

`\overline{v}=(\int v(t)dt)/(\int dt)`

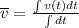
Using the given function of velocity and using the limits from t = 0 to t = 8 secs we get

`\overline{v}=(\int_(0)^(8)(3t^2-12t-15))/(\int_(0)^(8)dt)\\\\\therefore \overline{v}=(8)/(8)=1m/s`

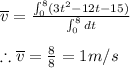
the average speed is calculated as

`Speed=(Distance)/(Time)`

`Distance=\int \sqrt{1+((ds)/(dt))^(2)}\cdot dt\\\\Distance=\int_(0)^(8)\sqrt{1+(3t^2-12t-15)^(2)}\cdot dt\\\\Distance=186.51m`

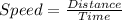
Hence the average speed is calculated as

`Speed=(186.51)/(8)=23.31m/s`