Question

Calculate the cell potential for a cell operating with the following reaction at 25 degrees Celsius, in which [MnO4^1-] = .01M, [Br^1-] = .01M, [Mn^2+] = .15M, and [H^1+] = 1M. The reaction is 2 MnO4^1-(aq) + 10 Br^1-(aq) + 16 H^1+(aq) --> 2 Mn^2+(aq) + 5 Br2(l) + 8 H2O(l)

Answer 1

Answer: The cell potential of the cell is 0.31 V

Step-by-step explanation:

We know that:

`E^o_((Br_2/2Br^-))=1.07V\\E^o_((MnO_4^-/Mn^(2+)))=1.51V`

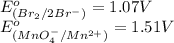
The substance having highest positive
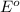`E^o` potential will always get reduced and will undergo reduction reaction. Here,
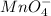`MnO_4^-` will undergo reduction reaction will get reduced. And, bromine will get oxidized.

Oxidation half reaction:
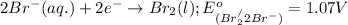`2Br^-(aq.)+2e^-\rightarrow Br_2(l);E^o_((Br_2^/2Br^-))=1.07V` ( × 5)

Reduction half reaction:
`MnO_4^-(aq.)+8H^+(aq.)+5e^-\rightarrow Mn^(2+)(aq.)+4H_2O(l);E^o_((MnO_4^-/Mn^(2+)))=1.51V` ( × 2)

The net reaction follows:

`2MnO_4^-(aq.)+10Br^-(aq.)+16H^+(aq.)\rightarrow 2Mn^(2+)(aq.)+5Br_2(l)+8H_2O(l)`

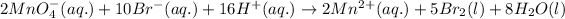
Oxidation reaction occurs at anode and reduction reaction occurs at cathode.

To calculate the
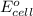`E^o_(cell)` of the reaction, we use the equation:

`E^o_(cell)=E^o_(cathode)-E^o_(anode)`

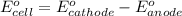
Putting values in above equation, we get:

`E^o_(cell)=1.51-(1.07)=0.44V`

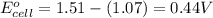
To calculate the EMF of the cell, we use the Nernst equation, which is:

`E_(cell)=E^o_(cell)-(0.059)/(n)\log ([Mn^(2+)]^2)/([MnO_4^(-)]^2* [Br^-]^(10)* [H^+]^(16))`

where,

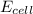`E_(cell)` = electrode potential of the cell = ?V

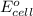`E^o_(cell)` = standard electrode potential of the cell = 0.44 V

n = number of electrons exchanged = 10

`[H^(+)]=1M`

`[Mn^(2+)]=0.15M`

`[MnO_4^(-)]=0.01M`

`[Br^(-)]=0.01M`

Putting values in above equation, we get:

`E_(cell)=0.44-(0.059)/(10)* \log(((0.15)^2)/((0.01)^2* (0.01)^(10)* (1)^(16)))\\\\E_(cell)=0.31V`

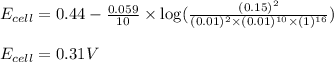
Hence, the cell potential of the cell is 0.31 V